Difference between revisions of "3^4"
(→Notation) |
Cutelyaware (Talk | contribs) m (Reverted edits by Blobinati (talk) to last revision by Cutelyaware) |
||
| (41 intermediate revisions by 2 users not shown) | |||
| Line 147: | Line 147: | ||
<li> Solve the remaining pieces using Roice Nelson’s piece-by-piece method or Raymond Zhao’s OLL/PLL approach. | <li> Solve the remaining pieces using Roice Nelson’s piece-by-piece method or Raymond Zhao’s OLL/PLL approach. | ||
</ol> | </ol> | ||
| + | |||
| + | ==Octachoroux Method== | ||
| + | This method is Rowan Fortier's 4 dimensional equivalent of the Roux method. It aims for a more intuitive blockbuilding approach, and requires fewer algorithms that need to be memorized. The name Octachoroux comes from the word octachoron (which is another word for tesseract) and Roux. | ||
| + | |||
| + | ===Prerequisites=== | ||
| + | <ul> | ||
| + | <li> Knowledge of how the puzzle turns, and Zhao Notation </li> | ||
| + | <li> Knowledge of blockbuilding and the Roux method on the 3^3 </li> | ||
| + | <li> Knowledge of names of 4d pieces and the concept of RKT </li> | ||
| + | </ul> | ||
| + | |||
| + | ===Summary of the Method:=== | ||
| + | <ul> | ||
| + | <li> First Block: Solve a 1x2x3x3 block using blockbuilding techniques </li> | ||
| + | <li> Second Block: Solve a 1x2x3x3 on the other side of the puzzle to complete your First 2 Blocks </li> | ||
| + | <li> CMLC: Orient and permute the corners of the U cell </li> | ||
| + | <li> L/R: Solve the Left and Right cells </li> | ||
| + | <li> M Slice: Permute the M slice </li> | ||
| + | </ul> | ||
| + | |||
| + | ===First Block=== | ||
| + | Pick the colour of which first block you will be starting with. If you normally start with White or Yellow on D and any colour on the side, that would make you x2yw colour neutral. <br> | ||
| + | Build a 1x2x3x3 block. You could solve the 2c pieces first, and then use the K cell to easily pair up pieces without disturbing your progress on the T cell. Then you can just bring those pairs onto the T cell and insert them using -K moves as normal 3^3 twists. <br> | ||
| + | Once this step is completed, hold the first block on the left, just as in normal Roux. <br> | ||
| + | [[File:Firstblock_2.png|400px]] [[File:Firstblock_1.png|400px]] | ||
| + | |||
| + | ===Second Block=== | ||
| + | Make the same 1x2x3x3 block, just on the other side. Start with the DR 2c piece. After that you can solve the other 4 2c pieces by bringing them to TU and doing RF TF' RF' to insert them. You can use many of the same tricks from the 3^3, such as hiding an edge in TDF and then rotating the U cell to bring the corner the edge pairs up with onto the T cell, then connecting them with M moves. RKT is necessary to insert pairs without messing up the first block. <br> | ||
| + | [[File:Secondblock.png|400px]] | ||
| + | |||
| + | ===CMLC (CO)=== | ||
| + | Bring the U cell to T, then use RKT to set up a layer so that it looks like a normal OCLL case, then bring the T cell to U. Hold that case so that it is in the D layer of the U cell, as shown in the image below, and use RKT variants of OCLL algorithms to orient those pieces. <br> | ||
| + | [[File:CMLC_CO1.png|400px]] <br> | ||
| + | Repeat this until all the corners are oriented. If you just have 1 corner left to twist, a good intuitive way to do this is to untwist 2 other corners, then use RKT to set that up in to a Sune case. You can also use the Monoflip algorithm described in the Sheerin-Zhao method above. <br> | ||
| + | [[File:CMLC_CO2.png||400px]] | ||
| + | |||
| + | ===CMLC (CP)=== | ||
| + | Now bring the U cell to T and use RKT to permute it like a regular 2x2x2 Rubik's cube. If you get a parity where a layer ends up being off by 180 degrees, use the RKT parity algorithm: <br> | ||
| + | TU UR T[LFU]' UK' TF RF UR RF' U[TR] <br> | ||
| + | It will look like this when it is done. Rotate the T cell back to the U cell <br> | ||
| + | [[File:CMLC_CP2.png|400px]] | ||
| + | |||
| + | ===L/R=== | ||
| + | Instead of orienting the edges like in 3^3 Roux, just go directly to solving the Left and Right cells of the cube. The reason why will become apparent later. <br> | ||
| + | First solve the 2c pieces with the L/R and U colour. <br> | ||
| + | Now you setup edges that need to go to L/R into the TDF spot with the L/R colour on the T cell and the U colour on the D cell. Then move the spot where that L/R edge needs to go above that edge and insert that piece using the RKT algorithm of M D2 M' D2 (2RK' TF' RK2 TF 2RK TF' RK2 TF) <br> | ||
| + | [[File:LR2.png|400px]] <br> | ||
| + | There are 8 edges total that need to be inserted for L/R do be complete. | ||
| + | |||
| + | ===M slice=== | ||
| + | [[File:M1.png|400px]] <br> | ||
| + | Now all you have to do is permute the M slice. This step is pretty similar to PLL from Sheerin-Zhao method, but with some key differences. <br> | ||
| + | <ul> | ||
| + | <li> Pieces have the same number of colours as they do on the 3^3. Corners pieces have 3, edges have 2, etc. </li> | ||
| + | <li> Pieces can look "mirrored" </li> | ||
| + | <li> There is no RKT parity </li> | ||
| + | </ul> | ||
| + | Now you can either use UR moves as U, U', U2 moves, and M slice rotations to do RKT (called URM), or rotate to bring one of the L/R sides to the T cell and use normal RKT, except you have to hold down 2 on your keyboard in order to do T moves. <br> | ||
| + | There are some interesting "parities" you might encounter that are impossible on both the 3^3, and the 3^3 last layer of CFOP 3^4. Such as: <br> | ||
| + | <ul> | ||
| + | <li> Corner pieces that look "mirrored" </li> | ||
| + | <li> Impossible Last Layer/CMLL(/whatever method you use) cases </li> | ||
| + | </ul> | ||
| + | If you solve the M slice using CFOP, then once you get to PLL, you can rotate the puzzle so that the U cell goes to T, and then orient the edges onto the T cell and then permute that like step 4c of the Roux method. <br> | ||
| + | If you solve the M slice using Roux, then look forward to impossible CO and CP cases from 2-look CMLL. <br> | ||
| + | An algorithm that is super useful here is a pure 2-flip of 3c pieces. I use M' U M' U M' U M' U2 M' U M' U M' U M' using RKT. | ||
Latest revision as of 02:19, 2 December 2022
Contents
Roice's Method
Roice's Method is a piece-by-piece solution that uses commutators that successively build on each other to solve one type of piece at a time.
A link to the method can be found here.
Ultimate Solution to a 3x3x3x3.
Additionally, Charles Doan has developed a system to implement this method. The tutorials can be found here.
Below is notation used by Ray Zhao.
Notation
Ray Zhao's Notation:
The notation is similar to that of the 3^3. There are 8 cells, six of them using the same letters as that in the 3^3: U (up), D (down), F (front), B (back), R (right), L (left). The near cell which is not visible, is named K, for kata. The far cell, which appears as the innermost cell, is named T, for top. (Thanks to Neodam22 for pointing out the problem!) Its name was changed from A to T since ana and kata are easier to confuse with each other than kata and "top".
Each cell in turn uses WCA Official Notation (standard notation).
The first letter determines the cell to click on. The second letter determines the sticker on the cell (is usually a 2C piece) to click on For example:
RK means to click the sticker on the right cell that joins to the near cell.
TF means to click the sticker on the far cell that joins to the front cell.
FT means to click the sticker on the front cell that joins to the far cell.
To state a set of all possible turns (clicks) of a cell, X- is used. For example: R- includes RU, RF, RD, RB, RT, and RK.
To state a set of all possible turns (clicks) of cells that are joined to the original sticker to be clicked, -X is used. For example, -R includes UR, FR, DR and BR, TR and KR.
Slice and wide turns can be notated with the 2c piece that you click on, plus the number you hold down to perform that move. For example, 2RK is like an M', and 12RK is like Rw'.
Rotation Notation:
This is the 2nd most widely used notation. It uses the same cell names from Zhao's Notation, but uses 3^3 x, y, and z rotations to be more intuitive.
If you wanted to make the F face of the T cell become the U face of the T cell, that would be Tx because it's rotating the T cell clockwise along the x axis.
One of the downsides of this notation is that edge and corner twist moves become longer. For example: T[UF] becomes Tz2x.
RKT
RKT is a technique that is used to execute moves that damage fewer pieces. By using RKT, the solver picks a cell that the solver wants to treat i.e. as a 3^3 (If it was a 4^4 you were solving, RKT would treat a cell as a 4^3). The main idea is to only use RK and T- moves.
For example,
- On a 3^3, you can do the sune algorithm: R U R' U R U2 R'. This is an OLL algorithm that can be used to orient corners, but is also able to permute edges (while breaking corners).
- On a 3^4, if you replace the algorithm above like so: R=RU, U=TU, you can see that the algorithm seems to have moved 3x1x1x1 blocks. That means that 2c, 3c and 4c are all moved. What if you only want to affect the 3c and 4c of the top 3x3x1x1 block of the T cell? (aka the TU ridge)
- Well, back on the 3^3, you can execute sune by doing only R turns and cube rotations. This becomes R z R z' R' z R z' R z R2 z' R'. Notice that the z turn brings the U face into the position of the R face, and the z' turn brings back the original R face.
- Now to convert the 3^3 algorithm from the previous step into an RKT algorithm, just substitute R=RK and z=TF. Notice how the T cell seems to be affected in the exact same way the 3^3 was affected in the last step; treating the T cell as a 3^3, it seems to undergo z and R turns.
Note that even though this method is called RKT, it is not limited to those types of turns. Thus, you can use LK and T- moves instead, or rotate your view and use RU and D- instead of RK and T-!
Sheerin-Zhao Method (Hybrid) V1
This method is an attempt to make a 4D analogue of the Fridrich/CFOP method. Using this method results in around 650 to 900 moves, even if no shortcut turns are used. This method needs significant improvement because of the move count required for the last layer.
Prerequisites
- Knowledge of how the cube rotates.
- The Fridrich Method (F2L/OLL/PLL). 2-look OLL/PLL is enough.
- Some commutators, especially the monoflip. (R' D' R D R' D R and its inverse)
- The notation described above
Summary of the Method
- Cross: Make a cross by solving 8 2C pieces on the far cell.
- F2L: Fill in F2L slots by joining F2L pairs (2C/3C) together and inserting them into their respective slots.
- S2L: Fill in S2L slots. This is done by moving a 3C piece and its respective 4C piece onto the farthest cell. Then, OLL algorithms are used to orient the pieces so that they can be joined using RKT moves. They are then inserted using modified RKT moves.
- OLL: Orient the LL 2C pieces, 3C pieces, then the 4C pieces using OLL-C (corner OLL) algorithms, such as the sune/antisune. Try to get as many corners oriented as possible as well. Setup moves are highly recommended here.
- Pre-PLL: Permute the 2C of the LL using U-perms.
- PLL: Solve the LL like a 3^3 by using RKT moves. (The cube is rotated at this stage)
- Parity: If the "top face" of the LL is 180 degrees off from the rest of the puzzle, use the RKT variant of the 180-degree-CW supercube center algorithm (R U R' U five times, OR L R U2 R' L' U twice).
Method
Cross
- Pick the colour that you will be using for the near cell (the cell not inside the viewpoint). In this example, cyan is chosen.
- Rotate the puzzle so that the cell with that specified colour is now the near cell.
- Intuitively place all -K (2C face) pieces oriented and permuted correctly.
This image shows the solved cross.
F2L
- Find any 2C piece that does not include a sticker with the colour of the far cell (i.e. grey).
- Find the 3C piece with the stickers that have the same colours of the 2C piece and of the near cell. For example, if the 2C piece's colours were red and yellow and the near cell piece was cyan, the 3C piece would be red, yellow, and cyan.
- Intuitively align the two pieces so that they lie on the same slice on the far cell.
- Join the pair together and insert the pair into the slot using -U moves.
- Repeat 11 more times.
Note: It is possible to insert the slot flipped. There are many shortcuts in forming pairs too. The image below shows the flipped pair (white-blue).
- Here is what it should look like when you are done:

S2L
- Find any 3C piece that does not include a sticker with the colour of the far cell (i.e. grey).
- Find its respective 4C piece (see F2L for details).
note: try finding pairs that are already on the far cell first. - If either piece is already inserted and there are no more pairs on the far cell, go down to step 6 and use the algorithm to take the piece out of the slot.
- Orient the pieces so that the same colours are on the far cell. Sune and antisune is used. Setup moves and RKT are a must.
- Join the pair together using RKT moves. Twist the far cell until the pair is aligned as shown below (i.e. the green-orange-white pair on the D cell):

It is possible for the pair to be oriented in two other ways. Make sure that the side colours of the S2L pair match the colours of the faces. Notice how the green and orange stickers match up with the side. - Now, the piece can be inserted using RKT. In this case, it is in the form of RU and D- instead of RK and T-, since you are treating the D cell as a 3^3. In the example shown above, since it is to the left of the slot from that viewpoint, it can be inserted using: (LU DT LU' DT') (LU' DT LU DT'). The next image shows the pair in place.

- Repeat 7 more times.
- Here is what it should look like when you are done (By now you should have used at most 450 moves):

OLL
- Use -U variants of OLL algorithms to orient the 2C pieces. (e.g. for line, FU RU TU RU' TU' FU')
Attempt to orient as many 3C pieces in this step as possible. - For any unoriented 3C pieces, orient them using -U variants of corner OLL algorithms such as the sune.
Note: if there is only one 3c piece left unoriented (see image below), place it so that it's facing you (see f2l flipped pair pic for reference).
Use this algorithm if the piece needs to rotate CW: [RK2 RU' TR2 TU' LT2 LU' TR2 TU']*2. For rotating the other way, just reverse the algorithm.

- Before starting to orient the 4C pieces, rotate the cube so that the up cell is now the far cell (T->U). The next image shows the transformation. (Notice the unoriented 3C piece. That is an error; orient all 3C pieces first!)
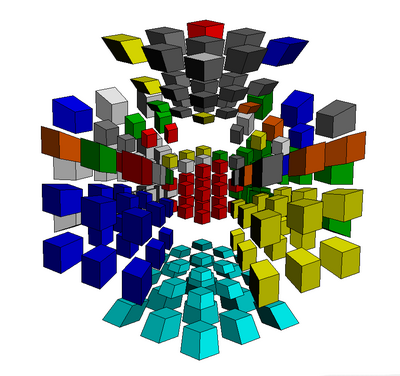
- Do U- moves so that the unoriented 4C pieces have their U cell sticker (i.e. grey sticker) NOT on the T cell.
- Use RKT variants of corner OLL algorithms to orient the 4C piece. If by the end of the algorithm the right cell isn't aligned with the rest of the puzzle, do TF, turn RK until the right slice realigns, then do TF'. Repeat this step and the previous one until all 4C pieces are oriented.
- If there is only one 4C piece left unoriented (see image below), place it so that it's facing you (see f2l flipped pair pic for reference).

Then, do BR', use the RKT variant of the monoflip, and do BR. The monoflip to rotate the U-layer sticker of the FULT piece from the L cell to the U cell is as shown: [R U R' U']*2 L' [U R U' R']*2 L. Do the inverse for the algorithm that rotates the U-layer sticker of the FULT piece from the F cell to the U cell. - When all LL layer pieces have been oriented, the T cell should be one uniform colour. Rotate the puzzle back (U->T). The image below shows the unrotated puzzle.
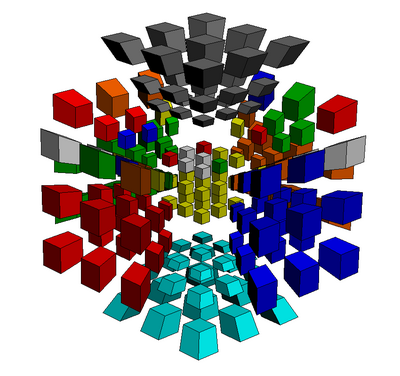
PLL
- Do T- moves to match as many 2C pieces as possible (At least 2). Then use the -U variant of the U perms to match the rest. (See the first step of OLL for an example of a -U variant.)

- From here, you use RKT moves to solve the rest of the puzzle like a 3^3. Parity: If the "top face" of the LL is 180 degrees off from the rest of the puzzle, use the RKT variant of the 180-degree-CW supercube center algorithm (R U R' U five times, OR L R U2 R' L' U twice).
Please note that this step is very inefficient and can take up to 200 moves on its own.
Charles Doan’s Method
This method consists of blockbuilding, as well as techniques from Roice Nelson’s method to solve the last few pieces. The method was intended for a low move count, as well as simply to serve as a unique method to solve the 4 dimensional Rubik’s Cube. Using this method as a beginner is strongly advised against. There will be complex concepts that will be very difficult to grasp, therefore it is advised that this method only be utilized by individuals who have relatively proficient experience for the 3^4 cube. This method will be making use of the notation established by Raymond Zhao.
Prerequisites
- To know how to solve the 4D Rubik’s Cube using Roice Nelson’s method.
- To be proficient at blockbuilding on a normal Rubik’s Cube.
- To have adequate experience for the 4D Rubik’s Cube.
Steps
- Solve a 2*2*2*2 cube.
- Expand the block to a 2*2*3*2.
- Create a full or semi-F2L on the inner face.
- Solve the First 2 Layers with or without missing 4-coloreds.
- Solve the remaining pieces using Roice Nelson’s piece-by-piece method or Raymond Zhao’s OLL/PLL approach.
Octachoroux Method
This method is Rowan Fortier's 4 dimensional equivalent of the Roux method. It aims for a more intuitive blockbuilding approach, and requires fewer algorithms that need to be memorized. The name Octachoroux comes from the word octachoron (which is another word for tesseract) and Roux.
Prerequisites
- Knowledge of how the puzzle turns, and Zhao Notation
- Knowledge of blockbuilding and the Roux method on the 3^3
- Knowledge of names of 4d pieces and the concept of RKT
Summary of the Method:
- First Block: Solve a 1x2x3x3 block using blockbuilding techniques
- Second Block: Solve a 1x2x3x3 on the other side of the puzzle to complete your First 2 Blocks
- CMLC: Orient and permute the corners of the U cell
- L/R: Solve the Left and Right cells
- M Slice: Permute the M slice
First Block
Pick the colour of which first block you will be starting with. If you normally start with White or Yellow on D and any colour on the side, that would make you x2yw colour neutral.
Build a 1x2x3x3 block. You could solve the 2c pieces first, and then use the K cell to easily pair up pieces without disturbing your progress on the T cell. Then you can just bring those pairs onto the T cell and insert them using -K moves as normal 3^3 twists.
Once this step is completed, hold the first block on the left, just as in normal Roux.


Second Block
Make the same 1x2x3x3 block, just on the other side. Start with the DR 2c piece. After that you can solve the other 4 2c pieces by bringing them to TU and doing RF TF' RF' to insert them. You can use many of the same tricks from the 3^3, such as hiding an edge in TDF and then rotating the U cell to bring the corner the edge pairs up with onto the T cell, then connecting them with M moves. RKT is necessary to insert pairs without messing up the first block.

CMLC (CO)
Bring the U cell to T, then use RKT to set up a layer so that it looks like a normal OCLL case, then bring the T cell to U. Hold that case so that it is in the D layer of the U cell, as shown in the image below, and use RKT variants of OCLL algorithms to orient those pieces.
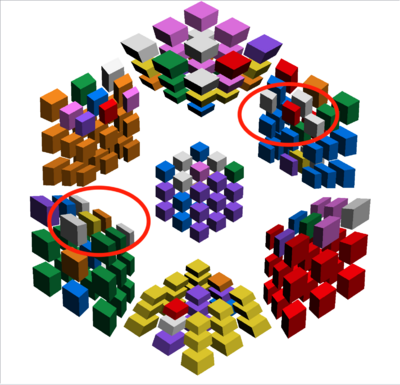
Repeat this until all the corners are oriented. If you just have 1 corner left to twist, a good intuitive way to do this is to untwist 2 other corners, then use RKT to set that up in to a Sune case. You can also use the Monoflip algorithm described in the Sheerin-Zhao method above.

CMLC (CP)
Now bring the U cell to T and use RKT to permute it like a regular 2x2x2 Rubik's cube. If you get a parity where a layer ends up being off by 180 degrees, use the RKT parity algorithm:
TU UR T[LFU]' UK' TF RF UR RF' U[TR]
It will look like this when it is done. Rotate the T cell back to the U cell

L/R
Instead of orienting the edges like in 3^3 Roux, just go directly to solving the Left and Right cells of the cube. The reason why will become apparent later.
First solve the 2c pieces with the L/R and U colour.
Now you setup edges that need to go to L/R into the TDF spot with the L/R colour on the T cell and the U colour on the D cell. Then move the spot where that L/R edge needs to go above that edge and insert that piece using the RKT algorithm of M D2 M' D2 (2RK' TF' RK2 TF 2RK TF' RK2 TF)

There are 8 edges total that need to be inserted for L/R do be complete.
M slice

Now all you have to do is permute the M slice. This step is pretty similar to PLL from Sheerin-Zhao method, but with some key differences.
- Pieces have the same number of colours as they do on the 3^3. Corners pieces have 3, edges have 2, etc.
- Pieces can look "mirrored"
- There is no RKT parity
Now you can either use UR moves as U, U', U2 moves, and M slice rotations to do RKT (called URM), or rotate to bring one of the L/R sides to the T cell and use normal RKT, except you have to hold down 2 on your keyboard in order to do T moves.
There are some interesting "parities" you might encounter that are impossible on both the 3^3, and the 3^3 last layer of CFOP 3^4. Such as:
- Corner pieces that look "mirrored"
- Impossible Last Layer/CMLL(/whatever method you use) cases
If you solve the M slice using CFOP, then once you get to PLL, you can rotate the puzzle so that the U cell goes to T, and then orient the edges onto the T cell and then permute that like step 4c of the Roux method.
If you solve the M slice using Roux, then look forward to impossible CO and CP cases from 2-look CMLL.
An algorithm that is super useful here is a pure 2-flip of 3c pieces. I use M' U M' U M' U M' U2 M' U M' U M' U M' using RKT.