Difference between revisions of "Markk's Physical Puzzles"
| Line 36: | Line 36: | ||
<br> | <br> | ||
== Moves == | == Moves == | ||
| − | The canonical moves on the physical 4-simplex are: trivial tip rotation, edge bimutation(binary permutation)/edge migration, center migration, simple rotations, compound | + | The canonical moves on the physical 4-simplex are: trivial tip rotation, edge bimutation(binary permutation)/edge migration, center migration, simple rotations, compound rotations and the gyro algorithm |
'''Edge Bimutation''' | '''Edge Bimutation''' | ||
| Line 53: | Line 53: | ||
---- | ---- | ||
| − | The gyro algorithm is easier on the physical 5-cell than on the physical pyraminx, because in the pinwheel edge configuration there is already a "flower" formed | + | The gyro algorithm is easier on the physical 5-cell than on the physical pyraminx, because in the pinwheel edge configuration there is already a "flower" formed. The gyro also has the same proprieties as the physical pyraminx gyro(mirroring the pinwheel and swapping the cell opposite the flower with the outside cell). |
| − | [[File:Physical simplex gyro.gif|thumb| | + | [[File:Physical simplex gyro.gif|thumb|centre|Animation showing the gyro on the physical 5-cell]] |
== Illegal and Impossible states == | == Illegal and Impossible states == | ||
| + | Like the physical pyraminx, the physical 5-cell can also be put in an ''impossible'' state. | ||
| + | <br> | ||
| + | [[File:Physical simplex impossible case.gif|thumb|centre|Animation showing the physical 5-cell being put in an ''impossible'' state]] | ||
Revision as of 09:55, 19 September 2022
Contents
2D Physical pyraminx
We can construct a physical pyraminx by taking a top-down orthographic view of the puzzle and then project it, making sure each piece type has the same shape in the projection so they are interchangeable. Doing this, we get an interesting 2D physical puzzle that looks like the wireframe of a tetrahedron projected in 2D, but with some of the lines disconnected. This is because we can't project a tetrahedron into 2D without unevenly distorting the shape or without having breaks in the shape.
Moves
The canonical moves on the physical 3x3 pyraminx are: trivial tip rotation, edge bimutation(binary permutation)/edge migration, simple rotation and the gyro algorithm
Edge Bimutation
Because of the projection, some of the edges/2Cs are disconnected, appearing connected to only one corner/3C, when in reality they are between two 3Cs, so the outer edges can be positioned so they touch any of its two corresponding 3Cs.This move is called edge bimutation(binary permutation) because the outer 2Cs can be moved between two positions.
Simple Rotation
This move is performed by first migrating all the edges of a 3C so they are all touching it, then rotating the 3C with the 2Cs. This move and the trivial tip rotation are the only scrambling moves of the pyraminx.
Gyro Algorithm
The gyro algorithm is a way of performing a "cube rotation" on the physical pyraminx, without affecting the state of the puzzle. The gyro starts with the outer edges in the shape of a pinwheel, then one edge is migrated such that it forms a "flower"(3Cs with all its 2Cs touching) opposite of the side that we want to become the outside face, then we move the remaining outer 3Cs and 2Cs on the "flower". After the gyro we can see that the face opposite the "flower" and the outside face have swapped places and the pinwheel shape is mirrored(anticlockwise if it started clockwise and vice versa).
Illegal and Impossible states
The physical pyraminx can not only be put in an illegal state, but it can be also put in an impossible state. An impossible state is a state that can't be reached on a true pyraminx, not even by dissassembling and reassembling the puzzle randomly. In this case, the impossible state of a physical pyraminx is when one or more of the 2Cs occupy the same slot.This state can be achieved because of the disconnects in the outer 2Cs with the 3Cs.
3D Physical Simplex
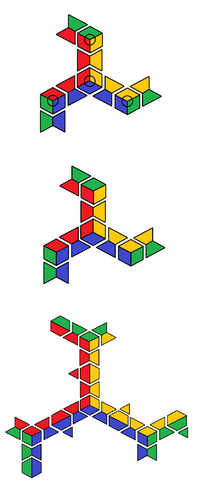
The 3D physical simplex/4D pyraminx/pentachoron/5-cell can be constructed in a similar way to the physical pyraminx, take the top-down orthographic projection of a pentachoron, making sure each piece type is the same shape so they are interchangeable.Doing this we end up with something that looks like the wireframe of a pentachoron with some lines disconnected. Another thing to note about the 4D pyraminx is that it has center pieces/1Cs, which the pyraminx doesn't have, so we have to account for them in the design.
Moves
The canonical moves on the physical 4-simplex are: trivial tip rotation, edge bimutation(binary permutation)/edge migration, center migration, simple rotations, compound rotations and the gyro algorithm
Edge Bimutation
Simple Rotation
There are 4 simple rotations. These moves are performed by first migrating all the 3Cs and all the 1Cs of a 4C so they are touching it, then rotating. Doing multiple simple rotations at once is called a compound rotation.
Gyro Algorithm
The gyro algorithm is easier on the physical 5-cell than on the physical pyraminx, because in the pinwheel edge configuration there is already a "flower" formed. The gyro also has the same proprieties as the physical pyraminx gyro(mirroring the pinwheel and swapping the cell opposite the flower with the outside cell).
Illegal and Impossible states
Like the physical pyraminx, the physical 5-cell can also be put in an impossible state.