Difference between revisions of "3-Block"
| Line 1: | Line 1: | ||
3-Block is a method designed for quickly speedsolving the [[3^4]]. The current speedsolving record of [[https://www.youtube.com/watch?v=gRWemTTFSik 7:43.33]] by HactarCE is set using this method. It was primarily invented by [[User:sonicpineapple|Luna]] and HactarCE, and has been described as "ZZ without EO". | 3-Block is a method designed for quickly speedsolving the [[3^4]]. The current speedsolving record of [[https://www.youtube.com/watch?v=gRWemTTFSik 7:43.33]] by HactarCE is set using this method. It was primarily invented by [[User:sonicpineapple|Luna]] and HactarCE, and has been described as "ZZ without EO". | ||
| − | + | =4/6 Cross= | |
| − | + | ||
Solve 4 out of the 6 cross pieces, with the cross colour being on the O cell. The unsolved cross spots will be on the Left and Right. | Solve 4 out of the 6 cross pieces, with the cross colour being on the O cell. The unsolved cross spots will be on the Left and Right. | ||
<br>[[File:4-6Cross.png|300px]] <br> | <br>[[File:4-6Cross.png|300px]] <br> | ||
| − | + | =Belt F2L= | |
Create and insert 4 F2L-a (2c3c) pairs into the 4/6 cross. This will solve 2/3 of the M slice. Because the Left and Right cells don't have their cross pieces, you can use them to aid with building and inserting the pairs. | Create and insert 4 F2L-a (2c3c) pairs into the 4/6 cross. This will solve 2/3 of the M slice. Because the Left and Right cells don't have their cross pieces, you can use them to aid with building and inserting the pairs. | ||
<br>[[File:BeltF2L.png|300px]] <br> | <br>[[File:BeltF2L.png|300px]] <br> | ||
| − | + | =Left= | |
Solve the Left cell. This is done in 3 blocks, hence the name of the method. The first block consists of the cross edge, followed by two 2c3c F2L-a pairs. This solves the middle column of the left cell. The final two blocks consist of a 2c3c pair, and two 3c4c pairs. | Solve the Left cell. This is done in 3 blocks, hence the name of the method. The first block consists of the cross edge, followed by two 2c3c F2L-a pairs. This solves the middle column of the left cell. The final two blocks consist of a 2c3c pair, and two 3c4c pairs. | ||
<br>[[File:Left.png|300px]] <br> | <br>[[File:Left.png|300px]] <br> | ||
| − | + | =Right= | |
Solve the Right cell. This is also done by breaking it up into the 3 blocks, except now you don't have an empty opposite cell to aid you in making pairs. | Solve the Right cell. This is also done by breaking it up into the 3 blocks, except now you don't have an empty opposite cell to aid you in making pairs. | ||
<br> [[File:Right.png|300px]] <br> | <br> [[File:Right.png|300px]] <br> | ||
| − | + | =OLC= | |
The last cell is oriented, as in [[Sheerin-Zhao Method]]. This is typically done by first orienting the 2c's, then 3c's, then 4c's, however the solver may wish to make use of setting up to big 3D OLLs, or use 4D specific algorithms if a case presents itself. | The last cell is oriented, as in [[Sheerin-Zhao Method]]. This is typically done by first orienting the 2c's, then 3c's, then 4c's, however the solver may wish to make use of setting up to big 3D OLLs, or use 4D specific algorithms if a case presents itself. | ||
| − | == | + | ==O2c== |
| + | Orienting the 2cs is a simple matter of using standard OLL algorithms. This can always be done in 2 algorithms or less. The first one should try to orient as many as you can while also making sure that there are 2 oriented opposite of each other. After that, a standard 3D case should appear. The image below would need the algorithm F U R U' R' F' (without RKT). <br> | ||
| + | [[file:2cOLL.png|300px]] <br> | ||
| + | |||
| + | =PLC= | ||
The last cell is permuted, as in [[Sheerin-Zhao Method]]. Do not forget to permute the 2c's first using EPLL algorithms. RKT is used to solve the last cell like a 3x3x3. | The last cell is permuted, as in [[Sheerin-Zhao Method]]. Do not forget to permute the 2c's first using EPLL algorithms. RKT is used to solve the last cell like a 3x3x3. | ||
Revision as of 13:37, 21 November 2022
3-Block is a method designed for quickly speedsolving the 3^4. The current speedsolving record of [7:43.33] by HactarCE is set using this method. It was primarily invented by Luna and HactarCE, and has been described as "ZZ without EO".
Contents
4/6 Cross
Solve 4 out of the 6 cross pieces, with the cross colour being on the O cell. The unsolved cross spots will be on the Left and Right.

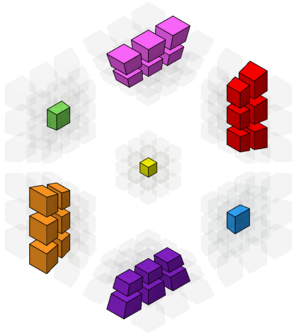
Belt F2L
Create and insert 4 F2L-a (2c3c) pairs into the 4/6 cross. This will solve 2/3 of the M slice. Because the Left and Right cells don't have their cross pieces, you can use them to aid with building and inserting the pairs.
Left
Solve the Left cell. This is done in 3 blocks, hence the name of the method. The first block consists of the cross edge, followed by two 2c3c F2L-a pairs. This solves the middle column of the left cell. The final two blocks consist of a 2c3c pair, and two 3c4c pairs.

Right
Solve the Right cell. This is also done by breaking it up into the 3 blocks, except now you don't have an empty opposite cell to aid you in making pairs.

OLC
The last cell is oriented, as in Sheerin-Zhao Method. This is typically done by first orienting the 2c's, then 3c's, then 4c's, however the solver may wish to make use of setting up to big 3D OLLs, or use 4D specific algorithms if a case presents itself.
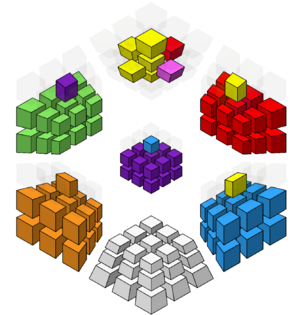
O2c
Orienting the 2cs is a simple matter of using standard OLL algorithms. This can always be done in 2 algorithms or less. The first one should try to orient as many as you can while also making sure that there are 2 oriented opposite of each other. After that, a standard 3D case should appear. The image below would need the algorithm F U R U' R' F' (without RKT).
PLC
The last cell is permuted, as in Sheerin-Zhao Method. Do not forget to permute the 2c's first using EPLL algorithms. RKT is used to solve the last cell like a 3x3x3.