Difference between revisions of "Hex9 Documents"
| (11 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | Back to [[MagicTile_Records]] main page | ||
| + | |||
| + | Back to [[Hex9]] | ||
| + | |||
| + | =Length 3= | ||
| + | This puzzle is the 16-coloured version of the hexagonal tiling. The slices are related to that of the Rubik's cube's or more specifically the Megaminx's, therefore the solution is not difficult. | ||
| + | |||
| + | =Length 3:1.2= | ||
Andrey: | Andrey: | ||
| Line 6: | Line 14: | ||
I just finished my {6,3} 9 colors, 3 layer factor = 1.29903810567 (the sweet spot Roice provided). For the edges, I used a 10-move commutator for 3-cycle, which is not too bad. It's actually easier than I expected yesterday. I notice you said your 3-cycle is 22-twist but re-orientation is 10-twist. That's a little weird. For me re-orientation is usually two 3-cycles. | I just finished my {6,3} 9 colors, 3 layer factor = 1.29903810567 (the sweet spot Roice provided). For the edges, I used a 10-move commutator for 3-cycle, which is not too bad. It's actually easier than I expected yesterday. I notice you said your 3-cycle is 22-twist but re-orientation is 10-twist. That's a little weird. For me re-orientation is usually two 3-cycles. | ||
| + | |||
| + | Andrey: | ||
| + | |||
| + | Yes, it's strange for me too. | ||
| + | |||
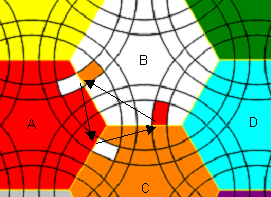
| + | Let's mark centers as | ||
| + | |||
| + | [[File:hex3-3-1.2-illustr.PNG]] | ||
| + | |||
| + | I've started with commutator [A,E']. Among other things it moves three edges around center D and changes orientation of two of them. So when I made [[A,E'],D^2] (10 twists), it was pure reversing of edges DF and DG. But I failed to make pure 3-cycle from it. | ||
| + | Then I tried [A,E]. Again, it moves 9 edges, and the best I made from it was 5-cycle [[A,E],C^2]. Third commutator converted it to 3-cycle: | ||
| + | [[[A,E],C^2],D^2]. Not very good, but enough for solving. | ||
| + | |||
| + | Nan: | ||
| + | |||
| + | Your reorientation algorithm is interesting. Using your notation, my 3-cycle is [[C,E],D] = (C,E,C',E'),D,(E,C,E',C'),D'. D can be replaced by D2, D3, D', etc to get some variations. | ||
| + | |||
| + | |||
| + | =Length 5= | ||
| + | |||
| + | Possible strategy | ||
| + | |||
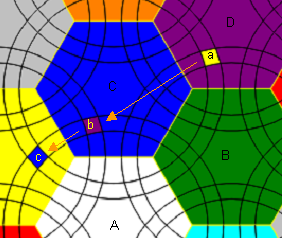
| + | (1) | ||
| + | Collect the edges first with normal twists then with the 3-cycle sequence | ||
| + | S1 = [[A,B2'],[D2',C]] , B and D second layer, A and C first layer | ||
| + | |||
| + | [[File:Eb_MT_Hex_9c_5_sq1.PNG]] | ||
| + | |||
| + | (2) | ||
| + | Do the face-edges with the 3-cycle sequence S2 = [A,B]^5 where A is layer 1 and B layer 2 | ||
| + | |||
| + | (3) | ||
| + | Do the edges as I have indicated in KleinsQuartic Document | ||
| + | |||
| + | (4) | ||
| + | Do the corners as I have indicated in KleinsQuartic Document | ||
| + | |||
| + | (5) | ||
| + | Do the face-corners with the 3-cycle sequence | ||
| + | S3 = [ C'DA2 [A,B'] A2'D'C , [A,B'] ] | ||
| + | all second layer turns except D | ||
| + | |||
| + | [[File:Eb_MT_Hex_9c_5_sq3.PNG]] | ||
| + | |||
| + | =other= | ||
| + | =other= | ||
Latest revision as of 13:47, 24 March 2011
Back to MagicTile_Records main page
Back to Hex9
Contents
Length 3
This puzzle is the 16-coloured version of the hexagonal tiling. The slices are related to that of the Rubik's cube's or more specifically the Megaminx's, therefore the solution is not difficult.
Length 3:1.2
Andrey:
With 9 colors first stage was easy, but edges are too much connected. The best thing that I could develop was 22-twist commutators for 3-cycle of edges and 10-twist for re-orientation of the couple of edges. And I had to remember them in normal and mirrored forms in all orientations of the plane. Terrible...
Nan:
I just finished my {6,3} 9 colors, 3 layer factor = 1.29903810567 (the sweet spot Roice provided). For the edges, I used a 10-move commutator for 3-cycle, which is not too bad. It's actually easier than I expected yesterday. I notice you said your 3-cycle is 22-twist but re-orientation is 10-twist. That's a little weird. For me re-orientation is usually two 3-cycles.
Andrey:
Yes, it's strange for me too.
Let's mark centers as
I've started with commutator [A,E']. Among other things it moves three edges around center D and changes orientation of two of them. So when I made [[A,E'],D^2] (10 twists), it was pure reversing of edges DF and DG. But I failed to make pure 3-cycle from it. Then I tried [A,E]. Again, it moves 9 edges, and the best I made from it was 5-cycle [[A,E],C^2]. Third commutator converted it to 3-cycle: [[[A,E],C^2],D^2]. Not very good, but enough for solving.
Nan:
Your reorientation algorithm is interesting. Using your notation, my 3-cycle is [[C,E],D] = (C,E,C',E'),D,(E,C,E',C'),D'. D can be replaced by D2, D3, D', etc to get some variations.
Length 5
Possible strategy
(1) Collect the edges first with normal twists then with the 3-cycle sequence S1 = [[A,B2'],[D2',C]] , B and D second layer, A and C first layer
(2) Do the face-edges with the 3-cycle sequence S2 = [A,B]^5 where A is layer 1 and B layer 2
(3) Do the edges as I have indicated in KleinsQuartic Document
(4) Do the corners as I have indicated in KleinsQuartic Document
(5) Do the face-corners with the 3-cycle sequence S3 = [ C'DA2 [A,B'] A2'D'C , [A,B'] ] all second layer turns except D