Difference between revisions of "KQ Documents"
From Superliminal Wiki
(→Tips for solving the Klein's Quartic length 3) |
|||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | Back to [[ | + | Back to [[MagicTile_Records]] mainpage |
| − | + | ||
| + | Back to [[Sept24|Klein's Quartic]] | ||
| Line 6: | Line 7: | ||
Stragegy 1 | Stragegy 1 | ||
| + | |||
This puzzle is the 24-coloured version of the heptagonal tiling {7,3}. The slices are related to that of the Rubik's cube's or more specifically the Megaminx's, therefore the solution is not difficult. Although, sometimes careful setup and insertion moves are required because of crowded space that forms after several centers are solved. | This puzzle is the 24-coloured version of the heptagonal tiling {7,3}. The slices are related to that of the Rubik's cube's or more specifically the Megaminx's, therefore the solution is not difficult. Although, sometimes careful setup and insertion moves are required because of crowded space that forms after several centers are solved. | ||
| Line 34: | Line 36: | ||
[[File:Edba_kq_macro_2.png]] | [[File:Edba_kq_macro_2.png]] | ||
| + | |||
| + | example: '''11''' 3'''1''' means | ||
| + | first color counter clock one unit | ||
| + | second color counter clock one unit | ||
| + | first color with clock three units | ||
| + | second color counter clock one unit | ||
Latest revision as of 16:19, 16 December 2011
Back to MagicTile_Records mainpage
Back to Klein's Quartic
Tips for solving the Klein's Quartic length 3
Stragegy 1
This puzzle is the 24-coloured version of the heptagonal tiling {7,3}. The slices are related to that of the Rubik's cube's or more specifically the Megaminx's, therefore the solution is not difficult. Although, sometimes careful setup and insertion moves are required because of crowded space that forms after several centers are solved.
Strategy 2
(a) solve the edges with simple commutators
(b) solve the vertices with the two sequences below
(with eventual pre- and post-paration; adjunction)
Sequence 1
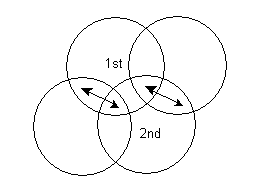
alternate first and second color twist to get a pair of vertex exchanges
11 11 11 11 11 11
bold = counter clock
Sequence 2
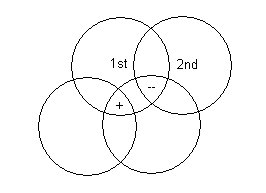
alternate first and second color twist to get a pair of vertex-turns
21 11 31 11 21 11 11 11 11 11 11
21 11 11 21 11 31 11 21 11 11 11 1
bold = counter clock
example: 11 31 means
first color counter clock one unit second color counter clock one unit first color with clock three units second color counter clock one unit